How To Draw A Root Locus

Example of root locus

Hither, we volition discuss an example with the root locus plot. As discussed, nosotros will follow the six rules of the root locus. We volition besides discuss the bear upon of the addition of pole and nix on the root locus.

Before starting with an example, permit's first discuss the steps to solve whatsoever problem on the root locus.

1. Find the number of poles, zeroes, number of branches, etc., from the given transfer functions.
2. Draw the plot that shows the poles and zeroes marked on information technology.
3. Calculate the angle of asymptotes and depict a separate sketch.
4. Observe the centroid and describe a separate sketch.
5. Find the breakaway points. These points can too exist in the form of complex numbers. We tin utilise the bending condition to verify such points in the complex class.
6. Summate the intersection points of the root locus with the imaginary centrality (or y-axis).
7. Calculate the bending of arrival and divergence if applicative.
8. Draw the final sketch of the root locus by combining all the to a higher place sketches.
9. We can also predict the stability and performance of the given system using the root locus technique.

Almost of the steps can be confusing. Let's discuss an case that will aid us to empathize the method to describe the root locus plot with the caption.

Instance: Draw the root locus diagram for a closed loop organisation whose loop transfer function is given by:

Thou(s)H(southward) = Thou/s(s + 5)(s + 10)

Also find if the system is stable or non.

Solution: We volition follow the process according to the steps discussed above.

Step one: Finding the poles, zeroes, and branches.

The denominator of the given transfer function signifies the poles and the numerator signifies the zeroes. Hence, there are 3 poles and no zeroes.

Poles = 0, -five, and -10

Zeroes = No zero

P - Z = 3 - 0 = 3

There are 3 branches (P - Z) budgeted to infinity and there are no open loop zeroes. Hence infinity will be the terminating bespeak of the root locus.

Step ii: Department of the real axis where the root locus lies.

There are iii poles, which are shown below:

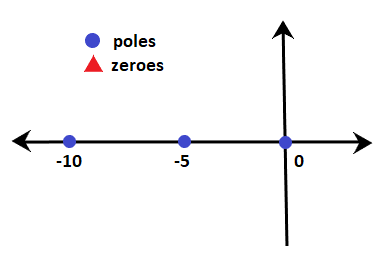
The section between 0 and -5 (for example, -iii.v) has only 1 pole on the correct-hand side. It ways that the sum of poles and zeroes on the side of the given point is 1.

Rule number 3 depicts that the section between 0 and -5 lies on the root locus. Similarly, department after -10 besides lies on the root locus. The department between -v and -10 has an even number of zeroes and poles on the right-mitt side. Hence, the root locus on the real centrality between -5 and -10 does not exist.

The breakaway point of the given organisation will lie between the section on the real centrality where the root locus exists, i.east., 0 and -5.

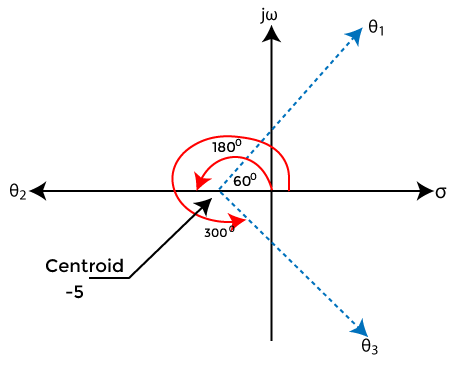
Step three: Angle of asymptotes.

Angle of such asymptotes is given by:

= (2q + 1)180 / P - Z

q = 0, ane, and 2

For q = 0,

Angle = 180/3 = 60 degrees

For q = 1,

Angle = 3x180/3 = 180 degrees

For q = 2,

Bending = 5x180/three = 300 degrees

Pace iv: Centroid

The centroid is given by:

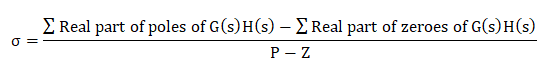
= 0 - 5 - ten - 0/3

= -fifteen/3

= -5

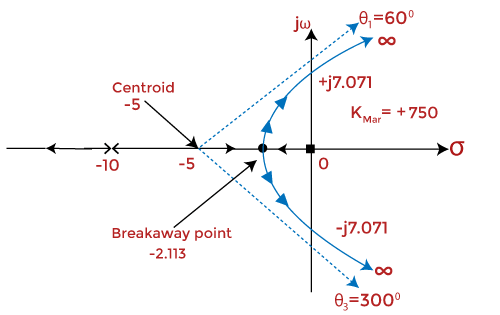
Thus, the centroid of the root locus is at -5 on the real axis.

The plot showing the centroid and the bending of asymptotes is given below:

Step v: Breakaway point

We know that the breakaway point will prevarication between 0 and -5. Let'southward observe the valid breakaway signal.

1 + G(due south)H(south) = 0

Putting the value of the given transfer function in the above equation, nosotros get:

i + K/s(s + 5)(s + 10) = 0

s(south + 5)(south + x) + K = 0

s(southⁱⁱ + 15s + 50) + K = 0

s^three + 15s² + 50s + Chiliad = 0

K = - sⁱⁱⁱ - 15s² - 50s

Differentiating both sides,

Dk/ds = - (3s² + 30s + 50) = 0

3s^two + 30s + fifty = 0

Dividing the equation by 3, we go:

southward² + 10s + 16.667 = 0

Now, nosotros volition find the roots of the given equation past using the formula:

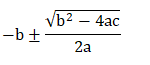
Using the value, a = 1, b = 10, and c = 16.667

The roots of the equation volition exist -2.113 and -7.88.

Amidst the two roots, only -2.113 lie between 0 and -5. Hence, it will be the breakaway point.

Let's verify by putting the value of the root in the equation K = - s³ - 15sⁱⁱ - 50s.

Grand = - -2.113 ³ - fifteen(-two.113)² - 50(-2.113)

Thousand = 48.112

The value of K is found to be positive. Thus, it is a valid breakaway point.

Stride 6: Intersection with the negative existent axis.

Here, we will found the intersection points of the root locus on the imaginary axis using the Routh Hurwitz criteria using the equation s³ + 15s² + 50s + Yard = 0

The Roth tabular array is shown below:

s3	ane	50
stwo	xv	K
s	15x50 - 1xK/Thou = 750 - 1000/K	0
s0	1000

From the third row s, 750 - K/K = 0

750 - K = 0

G = 750

From the second row s^two,

15 south² + K = 0

Putting the value of Kin the to a higher place equation, we get:

fifteen s² = -750

south² = -750/xv

s^two = -50

s = j7.071 and -j7.071

Both the point lies on the positive and negative imaginary axis.

Step 7: At that place are no complex poles present in the given transfer function. Hence, the bending of divergence is not required.

Step viii: Combining all the above steps.

The root locus thus formed after combining all the above steps is shown below:

Step 9: Stability of the organization

The system tin can be stable, marginally stable, or unstable. Here, we will make up one's mind the arrangement's stability for unlike values of G based on the Roth Hurwitz criteria discussed to a higher place.

The organization is stable if the value of Thou lies between 0 and 750. The root locus at such a value of M is in the left half of the s-plane. For a value greater than 750, the system becomes unstable, and it is considering the roots start moving towards the correct half of the s-aeroplane. But, at Thousand = 750, the system is marginally stable.

We can conclude that stability is based on the location of roots in the left half or right one-half of the south-airplane.

Touch on of the add-on of pole and nil on the root locus

Permit'south discuss the bear upon of the addition of poles and zeroes on the root locus.

Impact of the addition of pole

The impact of the adding pole to the left half of the s-plane will push the root locus towards the right side of the s-plane. We know that the system tends to be stable when the roots prevarication on the left one-half of the s-airplane. When the root locus moves towards right half, the stability reduces. It means that the addition of pole on the root locus will decrease the stability of the system. The range of 'K' and the proceeds margin f the system also decreases.

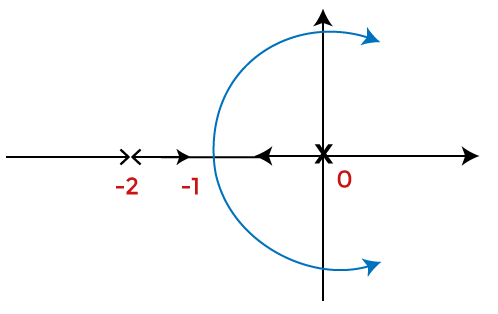
For case,

Consider the plot of the system K(s)H(s) = K/south(due south + two)(s + iv).

Now, let's add together due south = -six pole to the above system. The root locus plot will now appear every bit:

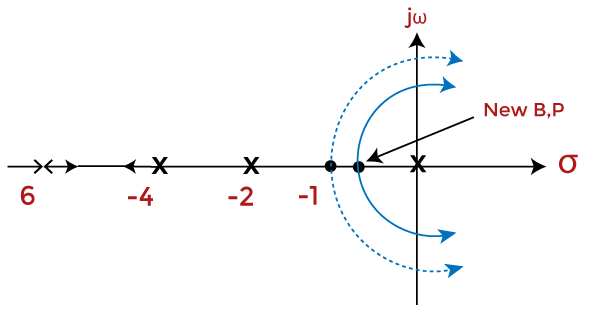
Thousand(s)H(south) = Thousand/s(due south + 2)(s + 4)(southward + 6).

We can notice that the improver of pole resulted in the root locus too shift towards the right-one-half of the s-plane.

Bear on of the improver of zippo

The touch of the adding zero will push the root locus towards the left side of the southward-aeroplane. We know that the organization tends to be stable when the roots lie on the left half of the s-plane. When the root locus moves towards left half, the stability improves. It means that the addition of nix on the root locus will increment the stability of the system. The range of 'K' and the gain margin f the system also increases.

Here, the root locus will shift towards the added cypher.

For example,

Consider the organization G(southward)H(s) = K(south + 4)/s(s + 2).

Now, let's add together zero s = -half-dozen to the above system. The root locus plot will at present appear as:

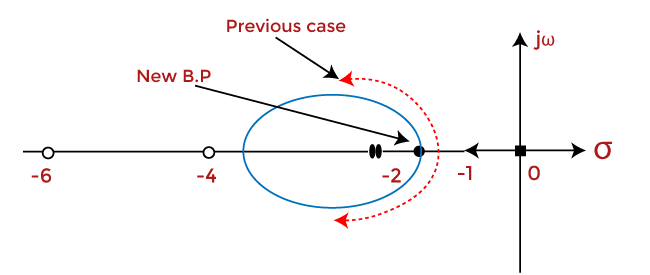
K(south)H(due south) = K(s + 4)(s + 6)/s(s + ii).

Nosotros can notice that the improver of pole resulted in the root locus too shift towards the right-half of the s-aeroplane.

---

Source: https://www.javatpoint.com/example-of-root-locus

Share this post